Tetsuji Matsuo received the B.E., M.E., and Dr. Eng. degrees from Kyoto University, Japan, in 1986, 1988 and 1991, respectively. He became a Research Associate, a Lecturer, and an Associate Professor at Kyoto University in 1991, 2001, and 2003, respectively. He is currently a Professor in the Department of Electrical Engineering, the Graduate School of Engineering, Kyoto University. His current research interests include computational electromagnetics, magnetic and material modeling.

Material models can be classified into physical and phenomenological models. Phenomenological models are constructed by fitting model parameters to measured data. They are determined using as few measured data as possible, but it is generally difficult for phenomenological models to predict material properties under conditions outside the measured data. In contrast, physical models can theoretically predict material properties based only on basic material constants. In this talk, after efficient and accurate phenomenological models are introduced, a physical model of magnetic materials is discussed.
The play model is a powerful phenomenological model. Its scalar model is mathematically equivalent to the classical Preisach model. It allows both the magnetic field and the flux density as its input to accurately describe the hysteretic property. The play model can be vectorized to construct an efficient vector hysteresis model [1], [2]. By combining the play model with a Cauer circuit, an accurate dynamic hysteresis model can be constructed [3]. Figure 1(a) shows simulated BH loops under PWM excitation, where the loops and losses are accurately reconstructed.
The development of a physical material model is a challenging task because of the multiscale nature of magnetic materials, where domain-wall behavior at the nm scale affects macroscopic properties at the mm/cm scale. Based on mesoscopic magnetic-domain modeling at the crystal-grain scale, a physical multiscale model of magnetic material was developed [4], [5]. It is an energy-based model that can handle the influence of physical factors in their energy forms. For example, magneto-mechanical interactions can be included by adding magneto-elastic energy. The multi-scale model successfully predicted stress-dependent properties of silicon steel [Fig. 1(b)].

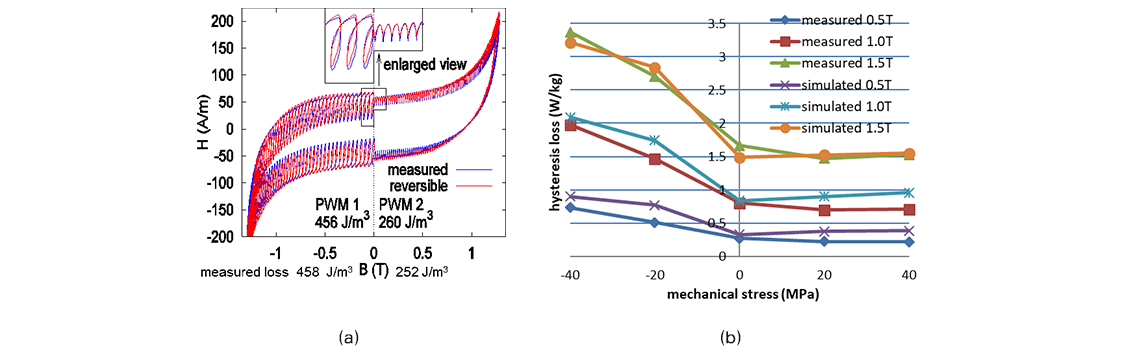
Fig. 1 Simulation results of non-oriented silicon steel: (a) BH loops under PWM excitation given by a phenomenological model and (b) stress dependence of hysteresis loss predicted by a physical model.

References:
[1] T Matsuo, “Anisotropic vector hysteresis model using an isotropic vector play model,” IEEE Trans. Magn., vol. 46, pp. 3041-3044, 2010.
[2] T Matsuo, M Miyamoto, “Dynamic and anisotropic vector hysteresis model based on isotropic vector play model for nonoriented silicon steel sheet,” IEEE Trans. Magn., vol. 48, pp. 215-218, 2012.
[3] Y. Shindo, T. Miyazaki, T. Matsuo, “Cauer circuit representation of the homogenized eddy-current field based on the Legendre expansion for a magnetic sheet,” IEEE Trans. Magn., vol. 52, 6300504, 2016.
[4] S. Ito, T. Mifune, T. Matsuo, C. Kaido, Y. Takahashi, K. Fujiwara, “Simulation of the stress dependence of hysteresis loss using an energy-based domain model,” AIP Advances, vol. 8, 047501, 2018.
[5] T. Matsuo, Y. Takahashi, K. Fujiwara, “Pinning field model using play hysterons for stress-dependent domain-structure model,” J. Magn. Magn. Mater., vol. 499, 166303, 2020.

Shiyou Yang received his M. Eng and PhD degrees in electrical engineering in 1990 and 1995, respectively. He is currently a full professor at the College of Electrical Engineering, Zhejiang university, China. His research interests include Computational Electromagnetics in both high and low frequency domains, and the application of numerical techniques in performance analysis and optimization of electronic and electromagnetic devices.
Shiyou Yang has been an active CEFC and COMPUMAG volunteer for over 30 years. He served in several important roles in the CEFC and COMPUMAG series conferences, such as the general Chair of IEEE CEFC2018; the Chair of International Steering Committee of IEEE CEFC from year 2020 to year 2022.

Metamaterials (MTM) is a novel artificial material, exhibiting exotic electromagnetic properties including negative permeability and or permittivity on some frequencies. The theory and applications of MTMs in high-frequency electromagnetics and optics have been widely and extensively studied. Recently, low-frequency MTM in near field power devices and system, covering wireless power transfer, magnetic resonance imaging, and magnetic shielding, has become a hot research topic. Nevertheless, as compared to a high-frequency MTM, the study of low-frequency MTM is still on the way in progressing. Moreover, the existing analysis methodology for a low-frequency MTMs is still basically inherited from those for high-frequency MTMs. The time domain computation methods for MTM-included electromagnetic systems are also oriented for electromagnetic waves instead of low-frequency quasi-static fields. Consequently, it is demanding to have a systematic exploration on the theoretical model and mechanism of a low frequency MTM, and its numerical modelling. In this point of view, this talk strives to present a systematic introduction on the working mechanism, the microcosmic and macroscopic model, the constitutive parameter abstracting approach, the time domain numerical method for MTM-consisted low-frequency near field systems and devices, the Euler-Lagrange method for low-frequency MTMs, and typical applications of low-frequency MTMs.